機率背後藏玄機改變抉擇展睿智｜星島教室

學習教室

更新時間：16:16 2023-11-23
發佈時間：16:16 2023-11-23

「機率」是數學領域的一門學問，它並非遙不可及，而是無處不在。由抽籤、擲骰子，以至天氣預報、金融投資，無不涉及機率。讀者們或許也有參加抽獎遊戲的經驗，懂得增加自己勝算小智慧，你就能成遊戲中的大贏家！

山羊問題

以下筆者將與讀者玩一個遊戲。

眼前有三扇緊閉的門，當中一扇門後面有汽車，另外兩扇門後面有山羊。若你幸運選中有車的門，便能榮升為車主。遊戲開始時，你隨機選了1號門。這時候，主持人打開3號門，讓你知道3號門後沒有車。主持人給予你改變最初選擇的機會，你會如何抉擇？

這是一道著名的謎題：「山羊問題」（Monty Hall problem）。在決定應否改變選擇時，不可單憑直覺或祈求上天眷顧，而是要好好計算機率。

如果你認為1號門和2號門的機率同是，改不改變選擇也無關緊要，那便錯了！當主持人打開3號門之後，汽車在1號門後面的機率是，而汽車在2號門後面的機率是。

1號門和2、3號門的對決

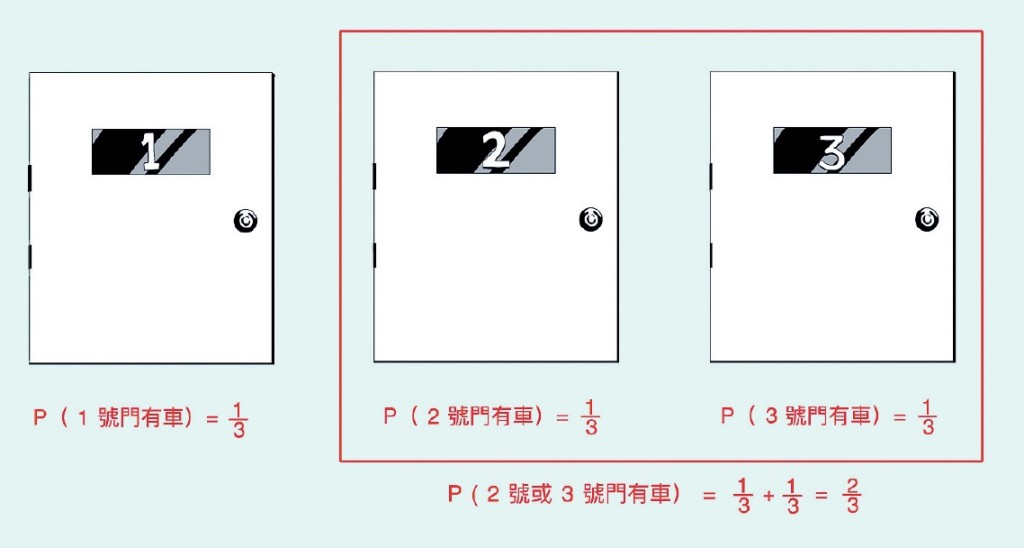
遊戲開始時，汽車可能在1號、2號，或3號門後，故1號門有車的機率為。同理，2號門和3號門有車的機率亦各自是。這意味着2號或3號門後有車的機率是（ + ）= 。

若玩家能在遊戲開始時，在「只選1號門」和「同時選2號和3號兩扇門」之間作出選擇，他必定會選後者。顯然，同時選兩扇門可以將他贏得汽車的機率由提升至。不過遊戲開始時，主持人並沒有給予玩家這兩個選擇；玩家只能選一扇門，而他隨機選了1號門。請注意，選擇1號門等同放棄2號和3號門，而2號或3號門後有汽車的機率是。

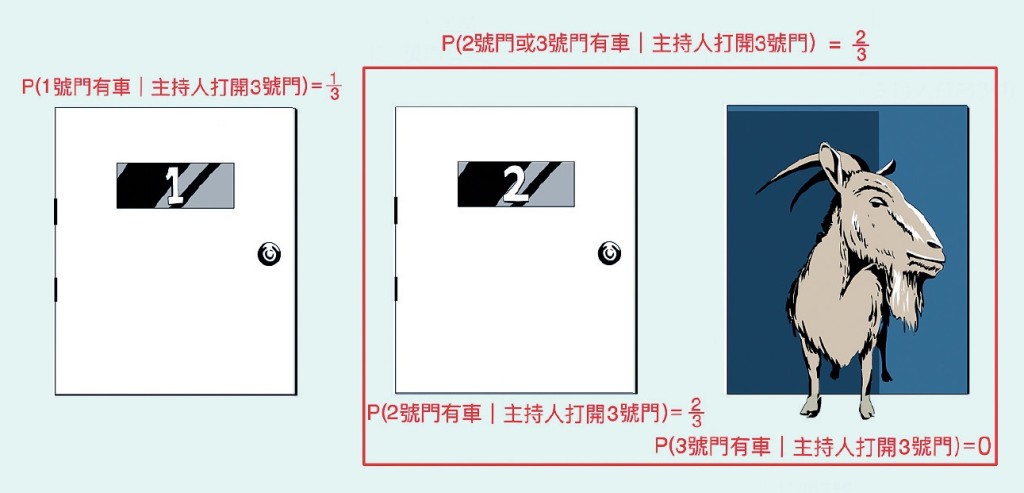
玩家選好1號門之後，主持人打開3號門，再給玩家一個改變選擇的機會。若玩家改變選擇，其實等同重新選擇本來放棄的2號和3號門。遊戲開始時，2號或3號門後有汽車的機率是。在主持人打開3號門之後，2號或3號門有車的機率仍然是；由於玩家已經知道汽車不可能在3號門後，所以3號門有車的機率會「轉移」給2號門，令2號門有車的機率變成。換言之，玩家在主持人打開3號門之後轉而選2號門，相當於在遊戲開始時，同時選2號和3號門。因此，改變選擇讓玩家有的機率贏得汽車！

改變永遠是最佳策略

事實上，無論主持人打開哪扇門，玩家都應該改變選擇來增加勝算。

上文假設3號門沒有汽車；現在，我們要考慮汽車的所有可能位置，所以必須撇除這個假設。正如下圖所示，汽車有3個可能位置：1號門、2號門和3號門。

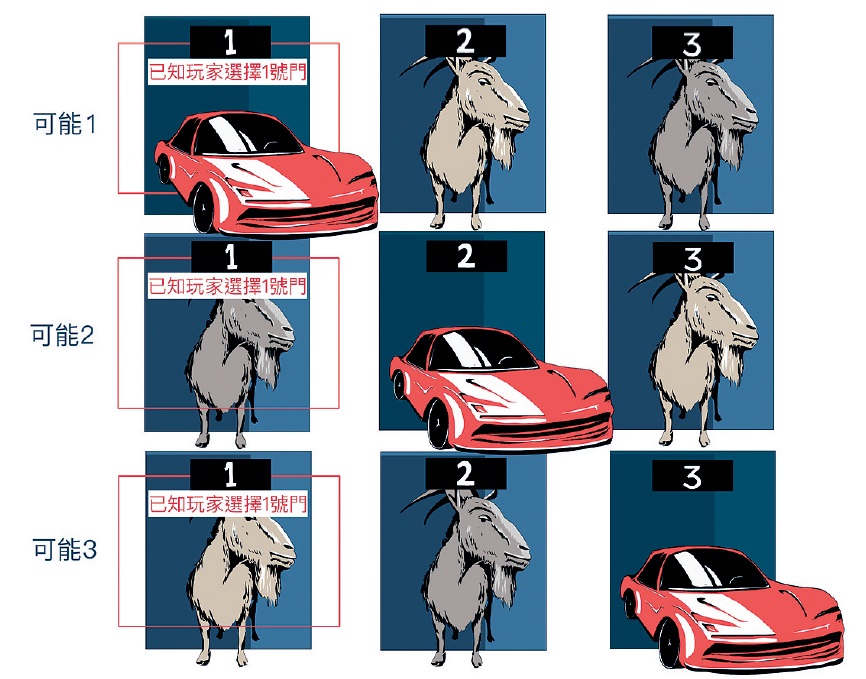
已知玩家選了1號門。玩家選好之後，主持人會打開一扇門，再問玩家要不要改變原來的選擇。主持人不能直接告訴玩家其選擇是否正確，所以主持人不會打開1號門，只會打開2號和3號門之間沒有車的那扇門。假如可能1號門為真，那麼主持人就會打開2號或3號門。如果玩家改變選擇，就不能贏得汽車。可是假如可能2號門為真，那麼主持人就只能打開3號門。若玩家改變選擇，就能贏得汽車。最後，假如可能3號門為真，主持人則會打開2號門。玩家改變選擇的話，就能贏得汽車。以上3個可能性中，玩家能在其中兩個情境中通過改變選擇贏得汽車；換言之，玩家改變選擇，有機率可以贏得汽車！

讀畢全文後，盼望讀者明白改變選擇能將贏得汽車的機率由增加至。事實上，「山羊問題」曝露了日常思考出現的盲點，我們要學會勤於思考、認真求證，自能撥開迷霧，增長智慧！